|
m-Canonic mirror curves
Paulus Gerdes Ethnomathematics Research Centre, C.P.915, Maputo, Mozambique; E-mail: pgerdes@virconn.com
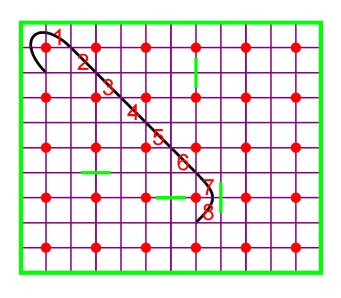
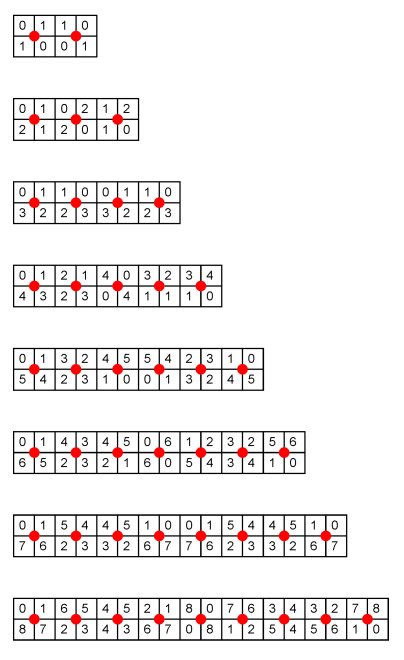
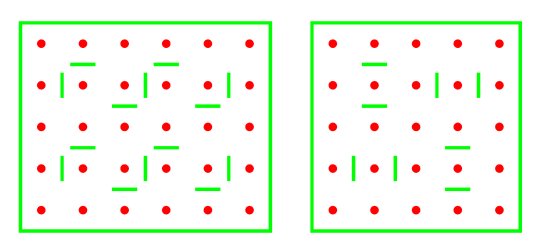
Mirror curves and Lunda-designs A mirror curve is the smooth version of a closed polygonal line reflected by the sides of a rectangle and possibly by one or more double-sided mirrors placed horizontally or vertically, midway, between neighbouring grid points belonging to a rectangular grid. The polygonal line makes angles of 45 degrees with the sides of the rectangle. The rectangular grid together with the double-sided mirrors constitutes a mirror design. Figure 1 presents an example of a mirror design and its corresponding mirror curve. This mirror curve is rectangle filling in the sense that it embraces all grid points and passes exactly once through each of the unit squares. We may enumerate the unit squares in the order in which the mirror curve passes successively through them. We may start the enumeration at the top left corner of the rectangular grid (Figure 2). 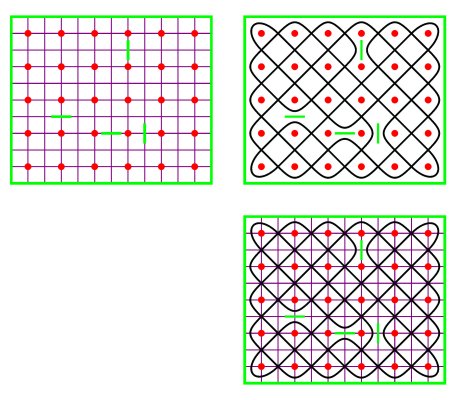
Figure 1
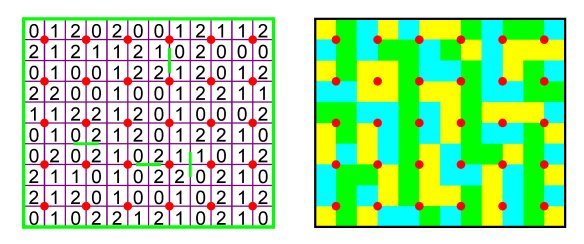
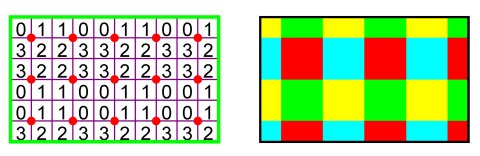
Figure 2 If one enumerates the unit squares modulo 2 (1, 0, 1, 0, 1, 0, ...), a {0,1}-matrix is obtained, as Figure 3a illustrates in the case of the mirror curve of Figure 1b. To the matrix corresponds a two-colour design (Figure 3b). Two-colour designs of this type are called Lunda-designs. Several properties of mirror curves and Lunda-designs are analysed in [1-17]. 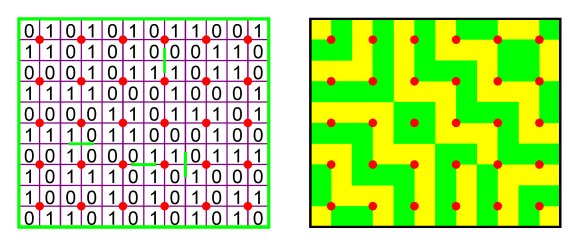
Figure 3
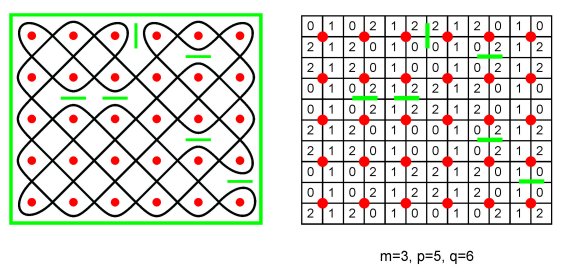
m-Valued matrices and m-colour designs Instead of enumerating the unit squares modulo 2, we may enumerate them modulo m, where m is a divisor of the total number of unit squares: 1, 2, 3, 4, …, m-1, 0, 1, 2, 3, … In this manner m-valued matrices and associated m-colour designs are produced [13-15]. Figure 4 presents the {0, 1, 2}-matrix and the corresponding 3-colour design produced by the mirror curve in Figure 1b. Figure 5 displays another mirror curve together with the 3- and 5-valued matrices it generates.
Figure 4
Figure 5
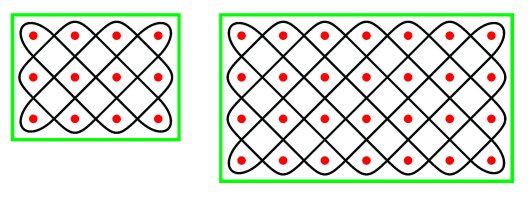
Simple mirror curves A rectangle filling mirror curve is called simple if there are no internal mirrors; the only reflections are in the sides of the rectangle. If the dimensions p and q of the rectangular grid RG[p,q] are mutually prime, a simple mirror curve smc[p,q] can be inscribed in the rectangle. Figure 6 presents the simple mirror curves inscribed in RG[3,4] and RG[4,7].
Figure 6 The unit squares through which a simple mirror curve inscribed in RG[1,m] passes can be enumerated modulo m. Figure 7 presents the m-valued matrices generated by smc[1,m] for m = 2, 3, 4, …, 9. In the case of even values of m, the matrices have also a vertical axis of symmetry. In the case of odd values of m, the matrices have a rotational symmetry of order 2. The sum of two numbers in the same column of any of these matrices is always equal to m-1.
Figure 7 What can said about the m-valued matrices generated by smc[p,q]? Figure 8 presents three examples. 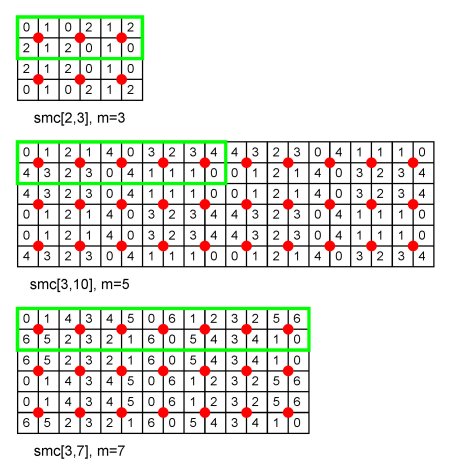
Figure 8
In each case m is a divisor of q and the m-valued matrix generated by smc[p,q] is built up by flipping horizontally and vertically the m-valued matrix generated by smc[1,m]. We may conjecture and prove the following theorem. Theorem 1:If p and q are mutually prime and m is a divisor of q, then the m-valued matrix generated by smc[p,q] may be obtained by flipping horizontally and vertically the m-valued matrix generated by smc[1,m]. This theorem implies that it is possible to calculate aij given i and j, where A[m,p,q] represents the m-valued matrix generated by smc[p,q]. On the one hand we have: If i = 4k or i = 4k+2, then aij = a1j ; If i = 4k+1 or i = 4k+3, then aij = a2j = m-1-a1j . On the other hand, we have: If j = 4mk+s, where 1£ s£ 2m, then a1j = a1s ; If j = 4mk+2m+s, where 1?s?2m, then a1j = a1(2m+1-s) . The m-valued matrices and m-colour designs generated by simple mirror curves will be called m-canonic matrices and designs, respectively. Figure 9 presents a 3-canonic design. Figure 10 presents a 4-canonic matrix and design.
Figure 9
Figure 10 The question to be analysed is the
following: do there exist non-simple mirror curves that generate m-canonic
matrices and designs.
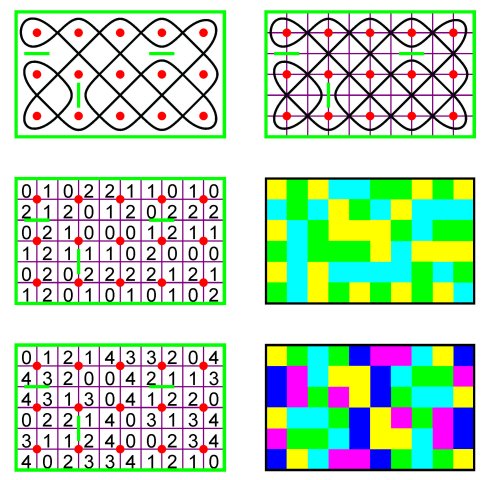
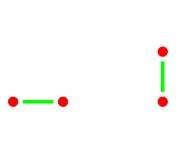
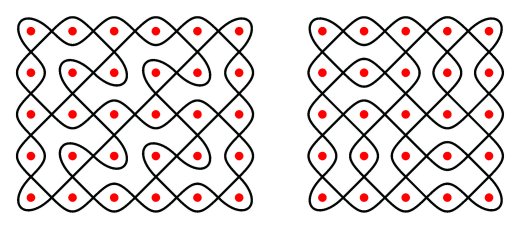
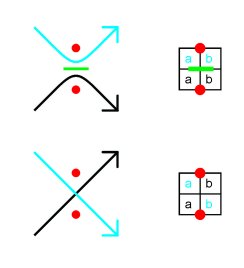
Regular mirror curves In [1] it was shown and in [2-4, 6] it was proved, that all mirror curves that belong to a particular class, called regular, generate 2-canonic and 4-canonic matrices and designs. Regular mirror curves are those mirror curves where any internal mirror can only be in one of the following two positions, either horizontally in the centre between two vertical neighbour grid points (Figure 11a) or vertically in the centre between two horizontal neighbour grid points (Figure 11b). In other words, if there exists at least one mirror horizontally between two horizontal neighbour grid points (Figure 12a) or vertically between two vertical neighbour grid points, then the mirror curve is not regular. Figure 13 presents pictogrammes from the Tchokwe in Northeast Angola and from the Tamil of South India [cf. 2-4] that are regular mirror curves as their respective mirror designs in Figure 14 show.
Figure 11
Figure 12
Figure 13
Figure 14
m-Canonic mirror curves The way m-canonic matrices and designs are built up implies that, if at specific places mirrors are introduced, the corresponding mirror curves – supposed they remain rectangle filling – produce the same m-canonic matrices and designs. Figure 15 presents an example.
Figure 15 The following theorem can be easily proven: Theorem 2:Consider a mirror design inscribed in RG[p,q], whereby one or more mirrors are placed horizontally in the centre between two vertically neighbour grid points or one or more mirrors are placed vertically in the centre between the (km)th and the (km+1)th grid point of any row (k=1, 2,…; m is a divisor of q). If the corresponding mirror curve is rectangle filling, then the mirror curve produces a m-canonic matrix and design. The proof is based on the fact that the placement of horizontal and vertical mirrors in the centre between (a, a+1) and (a, a+1) (see Figure 16), implying the elimination of a crossing, does not alter the m-valued matrix, provided that the resulting mirror curve continues rectangle filling.
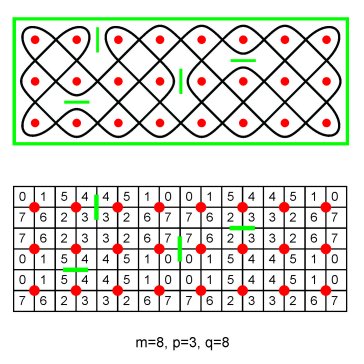
Figure 16 When m is an even number (m=2s), then also the placement of vertical mirrors in the centre between the (ks)th and (ks+1)th grid point of any row, does not change the m-valued matrix, supposing the resulting mirror curve is still rectangle filling. When m is a multiple of 4 (m=4t), the placement of vertical mirrors in the centre between the (kt)th and (kt+1)th leaves the m-valued matrix also invariant provided that the resulting mirror curve is rectangle filling. Figure 17 presents two examples. The special situation of multiples of 2 and 4 is a consequence of the fact that around each grid point there are four unit squares.
Figure 17 By consequence, we are arriving at a stronger version of the previous theorem: Theorem 3: Consider a mirror design inscribed in RG[p,q], whereby one or more mirrors are placed horizontally in the centre between two vertically neighbour grid points or one or more mirrors are placed vertically in the centre between the (kv)th and the (kv+1)th grid point of any row (k=1, 2,…; m is a divisor of q), where v=m if m is an odd number, 4v=m if m is a multiple of 4, and 2v=m is m is only an even number. If the corresponding mirror curve is rectangle filling, then the mirror curve produces a m-canonic matrix and design. A mirror design inscribed in RG[p,q] that is simple or that satisfies the conditions of Theorem 3 will be called m-canonic. If such a mirror design is monolinear, i.e. the corresponding mirror curve is rectangle filling, I will call the mirror curve m-canonic. In this way, we may reformulate Theorem 3: Theorem 3’:m-Canonic mirror curves generate m-canonic matrices and designs. Or stronger: Theorem 4: Only m-canonic mirror curves generate m-canonic matrices and designs. Like in the case of m=2,
that is in the case of Lunda-designs, it may be interesting to study further
properties of the
m-colour designs generated by mirror curves.
References [1] Paulus Gerdes, On ethnomathematical research and symmetry, Symmetry: Culture and Science, 1, 2 (1990), 154-170 [2] Paulus Gerdes, Geometria Sona, Universidade Pedagógica, Maputo, 1993-4 (3 volumes) [3] Paulus Gerdes, Une tradition géométrique en Afrique. — Les dessins sur le sable, L'Harmattan, Paris, 1995 (3 volumes) [4] Paulus Gerdes, Ethnomathematik dargestellt am Beispiel der Sona Geometrie, Spektrum Verlag, Heidelberg, 1997 [5] Slavik V. Jablan, Mirror generated curves, Symmetry: Culture and Science 6, 2 (1995), 275-278 [6] Paulus Gerdes, Lunda Geometry — Designs, Polyominoes, Patterns, Symmetries, Universidade Pedagógica, Maputo, 1996 [7] Paulus Gerdes, On mirror curves and Lunda-designs, Computers and Graphics, 21, 3 (1997), 371-378 [8] Paulus Gerdes, Geometry from Africa: Mathematical and Educational Explorations, The Mathematical Association of America, Washington DC, 1999 [9] Paulus Gerdes, On the geometry of Celtic knots and their Lunda-designs, Mathematics in School, 28, 3 (May 1999), 29-33 [10] Paulus Gerdes, On Lunda-designs and some of their symmetries, Visual Mathematics, 1, 1 (1999) (www.members.tripod.com/vismath/paulus/) [11] Paulus Gerdes, On Lunda-designs and the construction of associated magic squares of order 4p, The College Mathematics Journal, 31, 3 (2000), 182-188 [12] Slavik V. Jablan, Mirror curves, in Reza Sarhangi and Slavik Jablan (Eds.), Bridges: Mathematical Connections in Art, Music, and Science, Conference Proceedings 2001, Towson, 233-246, reproduced in: Visual Mathematics, 6 (2001) (www.members.tripod.com/vismath6/mir/) [13] Paulus Gerdes, Symmetrical Explorations Inspired by the Study of African Cultural Activities, in: T. Laurent & I. Hargittai (Eds.) Symmetry 2000, Portland Press, London (in press) [14] Paulus Gerdes, Variations on Lunda-designs, in: M. Emmer (Ed.), Matematica e Cultura 2002, Springer-Verlag, Milano (in press) [15] Paulus Gerdes, Lunda Symmetry where Geometry meets Art, in: M. Emmer (Ed.), The Visual Mind 2, MIT Press, Boston (in press) [16] Paulus Gerdes, From Liki-designs to cycle matrices: The discovery of attractive new symmetries, Visual Mathematics, 4, (2002) [17] Paulus Gerdes,
The
beautiful geometry and linear algebra of Lunda-designs, MERC, Maputo
2002 (preprint)
|