|
AN APPLICATION OF GRAPHS IN ARCHITECTURE Mª F. BLANCO and M. PISONERO
Name: Mª Francisca Blanco, Mathematician. Address: Department of Matemática Aplicada Fundamental, E.T.S. Arquitectura, University of Valladolid, Avenida de Salamanca s/n, 47014 Valladolid, Spain.
E-mail:
fblanco@maf.uva.es
Name: Miriam Pisonero, Mathematician. Address: Department of Matemática Aplicada Fundamental, E.T.S. Arquitectura, University of Valladolid, Avenida de Salamanca s/n, 47014 Valladolid, Spain.
E-mail:
mpisoner@maf.uva.es
Abstract:
One of the several and varied
applications of graph theory is found in Architecture and Design. Graphs
can be used, at least, in two different stages of the design. On one hand,
at the initial process of design, in order to draw in outline or to make
a sketch of the project, that establishes the relations and connections
between the different parts of it. On the other hand, as an instrument
of analysis of the finish or performed project, that allows a classification
of different styles or authors.
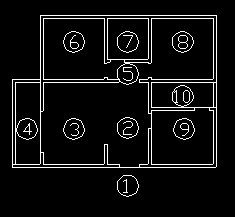
1 GRAPHS AND ARCHITECTURE Graphs provide a clear and simple representation of a great amount of data and different parameters related between them, which gives a better understanding of the project. Some aspects that can be made clear are: path economy for the potential users of the project, complementary use between the different rooms, level of privacy, … These grammatical rules of the architectural language are understood as a first step towards the project conception. Later on, they are translated into a mathematical language, through an algorithm, as a guide to follow, which uses graph theory. From a mathematical point of view, a graph G is a pair (V(G),E(G)), where V(G) is a non-empty finite set of elements, called vertices, and E(G) is a finite family of two elements sets of elements of V(G), called edges. If u and v are vertices of G, then an edge of the form {u,v} is said to join u and v and that u and v are adjacent. Two or more edges joining the same pair of vertices are called multiple edges, and an edge joining a vertex to itself is called a loop. A graph with no loops or multiple edges is called a simple graph, and in this case E(G) is a set. The degree or valency of a vertex u in a graph G (loopless), denoted by gr(u), is the number of edges meeting at u. A walk of length k in G is a sequence v0,e1,v1,e2,…,ek,vk of vertices and edges such that ei ={vi-1,vi} for all i, and we say that this walk is a walk between v0 and vk. Notice that if G is simple, a walk is completely determined by the sequence of vertices. When there is a walk between any given pair of vertices of a graph G (that is G is connected), the distance between two vertices u and v of G, denoted by d(u,v), is defined as the least length of the walks between them. The eccentricity of a vertex u in a graph G, denoted by e(u), is the maximum of its distances to other vertices. Observe that the degree of a vertex only depends on the local structure of that vertex, whereas the eccentricity of a vertex depends on the global structure of the graph. Let show how to use this theory in the study of a ground plan. For us the vertices will be the rooms and the edges the direct connections between each two rooms. Below we can see the ground plan of a small flat of 70 m2 and a graphical representation of the associated graph, which is a simple graph.
Figure 1. Ground plan of a small flat. The vertex assignation is: 1-exterior,
2-hall, 3-livingroom, 4-balcony, 5-corridor, 6-bedroom, 7-bathroom, 8-study,
9-kitchen and 10-dryingplace. The degree and eccentricity sequences are:
gr(1) = gr(4) = gr(6) = gr(7) = gr(8)
= gr(10) = 1, gr(3) = gr(9) = 2 and gr(2) =
gr(5) = 4; e(2) = 2, e(1) = e(3) = e(5)
= e(9) = 3 and e(4) = e(6) = e(7) = e(8)
= e(10) = 4.
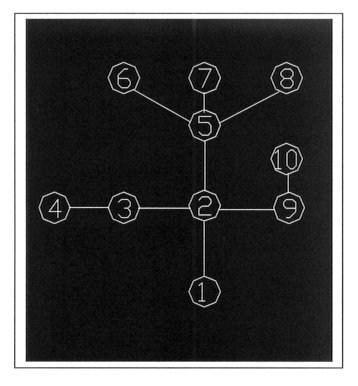
Figure 2. Graphical representation. Notice that the spaces with an only one direct connection are the 60% of the vertex set. The small size of the flat and the reduced number of the potential users are reasons that could explain both this and the existence of a unique entrance to the flat. The graph considered has three levels of degrees with a gap between degrees 2 and 4. The vertices with lowest degree correspond to spaces that require more privacy or because of noises or smells are more isolated, the vertices with medium degree correspond to main spaces and the vertices with highest degree correspond to circulation spaces. The central space, in terms of distances, is the hall. This fact is revealed by the lowest eccentricity of vertex 2. We also observe three levels of eccentricity without gaps: the lowest eccentricity corresponds to the central space, the highest eccentricity corresponds to the perimeter spaces and the medium eccentricity corresponds to the two main spaces, to a circulation space and to the exterior. The absence of cycles, that is the graph is a tree, is the usual way to design this kind of dwellings. One exception to this rule is found when the balcony can be accessible from two or more spaces. A proposal of study is to characterize
properties of the architectural language, by means of some mathematical
invariants associated to graphs, which allow us relating them with the
composition of the architectural or urban project.
References Gross, J., and Yellen, J. (1999) Graph Theory and its Applications, CRC Press, USA. Pellegrino, P., Coray, D., et al. (1999) Arquitectura e informática, Gustavo Gili, GG Básicos, Spain. Biggs,
N. (1996) Algebraic Graph Theory, Cambridge University Press, Great
Britain, (Reprint of the second edition, 1993).
|