|
THE PARTHENON’S SYMMETRY
Address: Anne Appelmans - Bulckens, Jalan Intan Ujung 75, Cilandak - Jakarta, Java Barat 12430, Indonesia E-mail: annepaul@cbn.net.id Fields of interest: Classical, Renaissance and Baroque Art and Architecture Publications: Bulckens, A.M. (1994) The Nature of Classicism, [Unpublished honours thesis], Geelong: Deakin University, 81 pp. Bulckens, A.M. (1998) Did Plato ever refer to a section in extreme and mean ratio in his writings?, Journal of Transfigural Mathematics, 3, no. 2, 27-31 and no. 3, 23-31. Bulckens, A.M. (1999) The Parthenon’s Main Design Proportion and its Meaning, [Ph.D. Dissertation], Geelong: Deakin University, 269 pp. Bulckens, A. and Shakunle, L. (1998)
Logic numbers and the music of Greek architecture, Journal of Transfigural
Mathematics, 4, no.1, 21- 47 and 53-57.
Abstract:
Commissioned by Perikles in a time when Athens knew power and prosperity,
the Parthenon (447-438 BC) represents the glory of Athens and the zenith
of Classicism. Although enticingly forming the subject of numerous works
of research, the understanding of several aspects of this temple to Athena
still remains tentative. Many scholars adhere to the view that the Parthenon
was designed and constructed in accordance with a simple 9:4 ratio. Although
this theory implies that the measurements of the Parthenon were calculated
from a basic measurement, it does not provide a convincing answer to one
of the Parthenon’s remaining riddles: what is the basic unit of measurement
used in the design of the Parthenon? Specifically, how long is the measure
of a Parthenon foot? The dissertation, The Parthenon’s Main Design
Proportion and its Meaning, offers new insights. Through an analysis
of the specific dimensions of the temple’s building parts, this thesis
establishes the measurement of a Parthenon Module and Parthenon Foot. It
then defines and explains the main design proportion of the Parthenon,
expanding the idea that the Parthenon was built with a 4:9 ratio. Rather:
the measurements and layout of the Parthenon’s building elements are based
on a Module, which attests to the symmetry of the Parthenon and which exalts
a 4:6 = 6:9 geometric proportion. This 4 – 6 – 9 theme is also found in
the symmetric number symbolism of the temple’s sculptural program.
1. SYMMETRY IN THE ARCHITECTURE OF THE PARTHENON Symmetry in architecture had a broader meaning in classical Greece than what is nowadays meant by architectural symmetry. Concerning symmetry and the proportioning of Greek temples, Vitruvius (c.10 AD) wrote: Symmetry is a
proper agreement between the members of the work itself, and relation between
the different parts and the whole general scheme, in accordance with a
certain part selected as standard ... In the case of temples, symmetry
may be calculated from the thickness of a column, from a triglyph, or even
from a module. (Vitruvius, p.14.)
Vitruvius explained
how in the Doric order, all temple parts depended upon the size of a module,
in a way that all the dimensions of the parts are determined by calculations
based upon it. He then explained many rules for the proportioning of a
Doric temple, although not every temple had to follow every rule. After analyzing
the Doric frieze of the Parthenon, I find that the following
Vitruvian rule concerning Doric temples applies: the size of the module
is equal to the width of a triglyph, and the width of a metope is 1.5 times
the width of a triglyph. (Vitruvius, p.112.)
With this rule applied to the Parthenon, it can be determined, and verified in figure 1, that theoretically, 36 modules constitute the entire length of the frieze of the Parthenon’s east façade, since the triglyphs (the blocks with 3 vertical grooves) are one module wide and the metopes (the square relief blocks between the triglyphs) are 1.5 modules wide. If it is assumed that during the first design stage – when the temple is still regarded as a perfectly upright structure without refinements such as the inward inclination of the columns – the length of this Doric frieze is set equal to the width of the stylobate (the upper platform upon which the temple columns rest), then the width of a module can be acquired by dividing the original stylobate width of 30866 mm by 36, which results in the width of this module being equal to 857.4 mm. Likewise, with a temple flank of 33 triglyphs and 32 metopes, it is clear that the flank is 81 modules long. When dividing the original stylobate length of 69493 mm by 81, one obtains a module of 857.9 mm, which is merely 0.07% longer than the module that was first calculated from the stylobate width. The average of these two calculations, then, leads to the one Module used in the overall design of the Parthenon. In the dissertation The Parthenon’s Main Design Proportion and its Meaning, it is shown that, based on one Module measuring 857.6 mm, the whole of the Parthenon was designed to an accuracy of 0.l5%. (It is noted that there is a similarity between this Module and one of the modules put forward by Ernst Berger. See Berger, pp.124-126.) If it is then assumed
that the width of a Module corresponds with two and a half times a ‘Parthenon
Foot’, all main building parts become measurable in the system of
feet and dactyls (with 16 dactyls constituting one foot), while
at the same time all main building parts are fully convertible and measurable
in Modules. Since I propose that one ‘Parthenon Foot’ is equal to 857.6
mm divided by 2.5, the result is a ‘Parthenon Foot’ of 343.04 mm.
Once this Module and Parthenon Foot are established, it becomes clear that
in the measurements, a 4 – 6 – 9 theme appears over and over again.
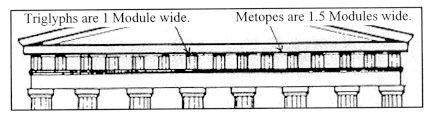
1. The Parthenon’s Doric frieze arrangement,
with its triglyphs and metopes.
In one case, even a 4² - 6² - 9² scheme is found in the use of the Module: the façade height (without pediment) measures 4² Modules, the stylobate width measures 6² Modules and the stylobate length measures 9² Modules. Thus the Modular measurements of some of the main building elements attest to the Parthenon’s symmetry. In this particular instance, the façade height (without pediment) stands to the stylobate width, as the stylobate width stands to the stylobate length, displaying the geometric proportion 4² /6²=6²/9². In the thesis, significant
weight is given to the exploration of the meaning of the temple’s main
design proportion. Because the Periclean Parthenon was built in the era
after Pythagoras had died c.497 BC, but before Plato was born c.428-427
BC in Athens, important aspects of Pythagoreanism are studied, especially
since in many respects Plato was also a Pythagorean. In this way the main
design proportion of the Parthenon is analyzed in accordance with its setting:
the Pythagorean era in Periclean Athens.
2. SYMMETRY IN THE PYTHAGOREAN NUMBER SYMBOLISM OF THE PARTHENON EAST FRIEZE AND EAST METOPES This thesis discovered
that there is a great link between Pythagoreanism and the Parthenon. For
the Pythagoreans, abstract ideas were symbolized by numbers. For example,
the number 4 could stand for reciprocity, justice, democracy, and in Athens
even victory, whereas the number 9 stood for tyranny and power. Also the
Olympian gods were symbolized by numbers. For example in Pythagorean number
symbolism, Poseidon, the ruler of the seas, was symbolized by the number
9. After analyzing many ancient Greek texts and works, I found that Athena,
as the patron of Democratic and Victorious Athens, was symbolized by the
number 4, while Athena ‘the Mother’ (of all Athenians) was denoted by the
number 6 and Athena ‘the Virgin’ by the number 7. The arrangement of the
twelve gods in the Parthenon (east) frieze is analysed – for the first
time – in light of this Pythagorean number symbolism. It will be shown
that in this east frieze, only the Parthenon’s protagonist gods sit in
their numerologically significant place. For example, Athena sits near
the center, in the sixth place when counting from the right, and in the
seventh when counting from the left. Poseidon, on the other hand, sits
in the ninth place when counting the seated gods from the left, whereas
in the east metopes he is depicted in the ninth metope when counting from
the right. Also, the fourth metope, read from the left as well as from
the right, highlights Victory. One can start to understand the underlying
message of the east metopes and the sculptural tableau with its 12 seated
gods by ‘reading’ the meaning of its number symbolism from left to right
and right to left. When thus analyzing this sculptural-numerical symbolism,
one surmises that the 4 – (6 -7) – 9 theme and its symmetry provide the
clue to the understanding of the meaning of the Parthenon.
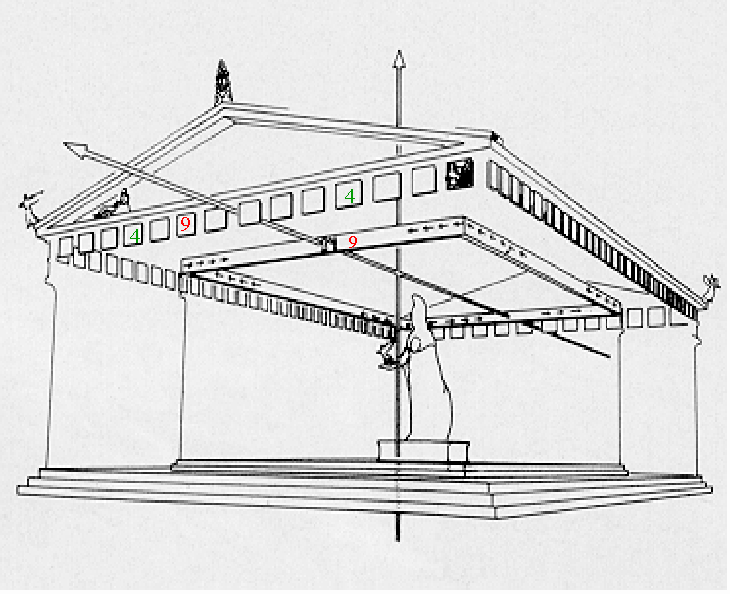
2. Symmetry of the number symbolism around the central axis of the Parthenon In all, this 4 –
6 – 9 theme pervades the entire Parthenon: in the symmetry of the architectural
elements it leads to the geometric proportion 4:6 = 6:9. In the sculptural
program of the temple’s east front it constitutes the core of the 4 – (6
-7) – 9 symmetric number symbolism.
References Berger, E., ed. (1986) Parthenon-Kongress Basel, 2 Vols, Mainz: Philipp von Zabern. Vitruvius (1960)
The
Ten Books on Architecture, Trans. from Latin by M. Morgan, New York:
Dover Publications.
|