Name: Dirk Huylebrouck, Mathematician, (b. Ghent, Belgium, 1957).

Address: Department of Architecture, Hogeschool W&K, 65-67 Paleizenstraat, Brussels 1030, Belgium. 

E-mail: dirk.huylebrouck@pi.be

Fields of interest: Algebra, mathematical tourism, etnomathematics (also space science).

Publications and/orExhibitions: - Research about matrices over rings symmetry. Most recent one: Generalized Inverses of a Sum with Radical Element, Applications, Linear Algebra and its Applications, 246: 159-175 1996.

- General mathematical texts. Most recent one: Mathematical lung model (about Katachi-ISIS member Takaki's research), short contribution in EOS-magazine, February 2001.

- Editor of The Mathematical Tourist in The Mathematical Intelligencer. Most recent contribution: Alphabetic Magic Square in a Medieval Church, by Aldo Domenicano and Istvan Hargittai, Winter 2000.

- Etnomathematics, about the oldest mathematical object, and its programmed odyssey in space. See: http://193.75.136.15/~dhuylebrouck/Ishango_web/Ishango_web.htm

- Organizer of a forthcoming ISIS-related seminar. See: http://www.matomium.org. 
 
 

Abstract: The golden number f arises when a line segment of length x (>1) is divided into pieces of lengths 1 and x-1, such that x = 1/(x-1), of which f = 1.6180... is the positive solution. The golden rectangle of width 1 and length 1.618… is said to be the most elegant, but as G. Markowsky pointed out, the statistical proofs for this popular assertion are not reliable. Nevertheless, the present paper will try to provide an answer to the question that the golden section corresponds to an optimal solution. It could reboot the mathematical career of the golden section.
 
 

1. The golden number

The golden number f (or golden section, mean, or ratio or divine proportion etc.) arises when a line segment of length x (>1) is divided into two pieces of lengths 1 and x-1. This division must be such that the whole length stands to 1, as 1 is to the remaining piece, x-1. Thus, the ratio x/1 must equal the ratio 1/(x-1). This produces the equation x²-x-1 = 0, of which (1+Ö5)/2=1.6180... = f is the positive solution; note that f - 1= f^-1 = 0.618… More generally, the positive roots of x²-nx-1 = 0 yield the family of "metallic means", for n = 1, 2, … For n = 2, it is the silver mean s_Ag=1+Ö2, etc. 

The properties of these numbers have been described extensively (for a comprehensive survey, see De Spinadel). Of course, the diagonal of a rectangle with length 2 and width 1 corresponds to the "irrational part" Ö5/2 of the golden section, but this is so obvious that it is hardly a 'mathematical application'. Still, the Fibonacci series 1, 1, 2=1+1, 3=2+1, 5=3+2, 8=5+3, 13=8+5, … is linked to f, since the quotient series, formed by of each term divided by the previous one, tends to it. The numbers 2, 3, 5, 8, 13, etc. yield many beautiful applications, when mixed with a portion of fantasy. Furthermore, the geometric properties of the equilateral triangle with a top "golden" angle of 36° yield another large category of interpretations. Since a pentagon has related angles, there are various often-surprising forms. Together with P. Labarque, the author recently introduced "golden gray", containing 61.8% pure light (the remaining being "black"). It lead to one of the very few devices to determine the golden number experimentally. 
 
 

2. The most elegant (golden) rectangle

To some authors, an explanation for the exceptionality of the metallic means is found in their representations as continued fractions, while some point to its emergence in proportions in the human body. Yet, these justifications do not use the approved mathematical language, to state it gently. Others turn to the golden rectangle of width 1 and length 1,618... It can be subdivided in smaller and smaller squares, and a spiral neatly fits into it. However, this is not so exceptional as often presented in introductory textbooks. Another justification of the importance of the golden rectangle would be its use in various designs. The Parthenon for instance would fit "exactly" in such a golden rectangle. Yet, a comparison of the various illustrations given in literature show this is a rather loose statement. Of course, painters and sculptors often subdivide their (rectangular) canvas or stone into proportions, and 3-5 or 5-8 arrangements are frequent. This provides a connection to the Fibonacci numbers. Yet, 2-4-8 schemes are popular too, and even used by great masters such as Seurat, Monet or Cézanne. It would be hard to prove that the Fibonacci subdivisions lead to the "most" beautiful artworks. 

The very few valid statistical experiments about the golden rectangle do not seem to confirm a preference for the golden rectangle. As G. Markowsky pointed out, it is not indisputable that one can pick out the "most elegant" (golden) rectangle from an arbitrary list. In spite of these vigorous considerations in disfavour of the golden section, many mathematicians continue to spread the myth, while others encounter it. Mathematicians may be somewhat biased about the subject. A moderate conclusion comes from a psychologist, Christopher Green. "Although many researchers have concluded that the effect is illusory", says Ch. D. Green, "more carefully conducted studies have fairly consistently shown, that there is, in fact, a set of phenomena that require explanation, though no one has yet produced an explanation, both adequate and plausible, that has been able to stand the test of time." 
 
 

3. Optimal solutions

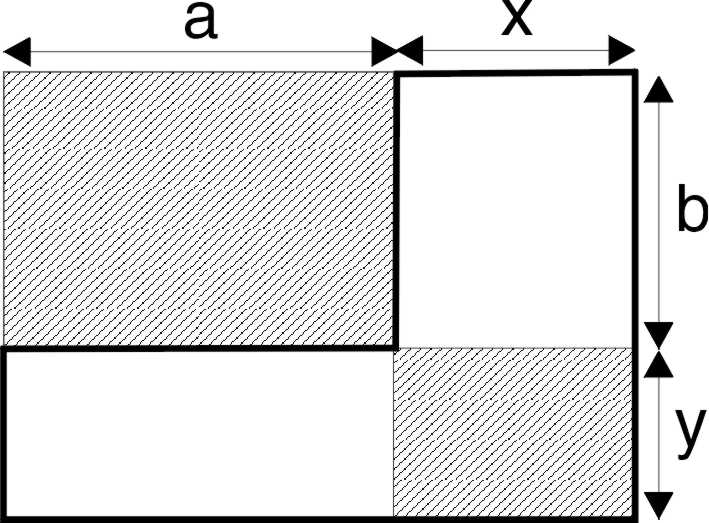
Here is an attempt to describe that (in)famous golden rectangle. It uses the common mathematical vocabulary, starting with a function to describe a geometric construction. Then, its derivative is set equal to zero, in order to find exceptional solutions. It appears that they are the golden number, its inverses or opposites. For a rectangle of arbitrary length a and arbitrary width b, we increase a by x and b by y (see Fig. 1). This creates two rectangles on the main diagonal (in gray), and two rectangles on the border (in white). The extended area, made up by the rectangles on the border and the added grey rectangle, is xb + ya + xy (surrounded by a tick black line). We compare this area ab +xy on the main diagonal (shaded).

It produces a function f(x, y) = (xb+ya+ab)/(ab+xy). Its extreme value is computed through f '_x = 0 and f '_y = 0, or y² –by – b² =0 and x² –bx – b² =0. 

The solution yields the possibilities: x = a(1±Ö5)/2 or and y = b(1±Ö5)/2, of which only the positive signs yield positive lengths x and y (an interpretation for the negative values could be given though). Now (af, bf, f) corresponds to a saddle point, while its z-value is the golden number, independently of the value of a and b. This could have been expected, as an initial division by a and by b would not have influenced the result. 

The fact that we get a saddle point is remarkable enough to point out the particularity of the golden section. Since it does not correspond to a maximum, another approach may be of interest. We can simply start with a square (a=b=1). The rectangle on either sides should not be too long nor too high; thus, for reason of symmetry and because of the previous experience, we could propose to take x=y. The extended area is compared to the area of the squares on the diagonal (in grey), and this is given by a function g(x)=2(2x+x²)/(1+x²). Its derivative is -2(x²-x-1)/(1+x²)², annihilating for x = 1.618… and this corresponds to a maximum. Thus, if we want to extend a square by another square to form a larger square, the added area is maximal, with respect to area of the two squares, if the golden section is used (see Fig. 2). 

The silver section can be obtained through such an optimization procedure. If the given rectangle is a unit square, the area cut off at one side is now compared to the total area of the two squares on the diagonal. The silver section is the positive solution of s'(x)=0, where s(x) = (x+x²)/ (1+x).

The expressions for the s(x), g(x) and f(x,y) functions were inspired by completely different mathematical problems (see Huylebrouck 2001). Yet, the given formulation seems to correspond to what was probably intended by the expression of "optimal solution", as given by so many authors, and refuted by others. It seems but a rephrasing exercise, using mathematical vocabulary, but it could help to reboot the mathematical career of the golden section.
 
 

References

Green, Christopher D. (1995) All that glitters: A review of psychological research on the aesthetics of the golden section, Perception, 24, 937-968.

Huylebrouck, D. (2001) Similarities in irrationality proofs for p, ln2, z(2) and z(3), American Mathematical Monthly, No. 3 [March]; cf. http://www.maa.org/pubs/monthly_mar_01_toc.html

Huylebrouck, D. and Labarque, P. (2000) Symmetric partition of colours on a rotating disk and the golden number, Abstracts: Alhambra 2000, Granada, Spain, July 3 – 7, 2000, 217-218. 

Huylebrouck, D. and Labarque, P. (2001) Colourful errors, Accepted for the Mathematics and Design Conference, Melbourne, Australia, July 3 – 7, 2001.

Markowsky, George (1992), Misconceptions about the golden ratio, The College Mathematics Journal, 23, No.1 [January], 2 - 19.

Spinadel, Vera W. de (1998) From the Golden Mean to Chaos, Buenos Aires, Argentina: Nueva Libreria S.R.L.