|
FOLK ART AND SYMMETRIES OF PERMUTATION - GENERATED SIGNS GEORGE LUGOSI Name: George Lugosi (b. Budapest, Hungary, 1936) Address: R&D&I, 2 Union Street, Kew 3101, Victoria, Australia E-mail: g.Lugosi@hfi.unimelb.edu.au Field of interest: Patterns, forms, analogical thinking, crystallography, geometry, (sailing, gliding, "sci-fi") Publications: Benapozás vizsgálata, [Investigating the Sun-path in a room, in Hungarian] M?vészet, 1977, 3 Szabadág=semmibe vett szükségszerüség? [Is freedom = ignored necessity? in Hungarian] Muvészet, 1978, 6 Patterns based on permutations, Symmetry: Culture and Science, Vol. 3 No. 2 (1992) More investigation on permutation-generated
patterns, Symmetry: Culture and Science, Vol. 6 No.2 (1995)
Abstract:
Looking old buildings or folk art, especially cross-stich patterns, we
can find returning patterns which are used in different geographical areas.
It is interesting to see that these patterns consist of rather simple signs
which are fitting to a permutation generated sign system. Investigating
this system, we can find symmetries, which are easily visible. If we use
a sign or a group of signs as a building block, we can build higher organised
symmetries, which are recognisable in the folk art.
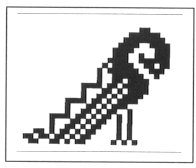
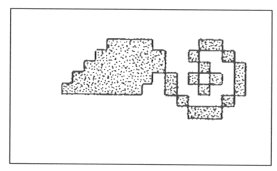
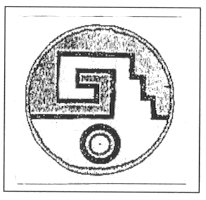
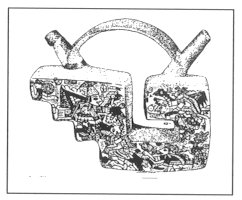
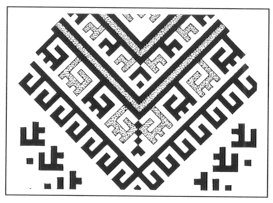
1. SOME IMPORTANT PATTERNS It is a remarkable fact that in the folk art we can find certain elements and patterns, which are characteristically returning again and again. Surprisingly, some of them looks like connected to each other and we can find them in different ages and very different geographical arias. Let us see some examples. In Fig. 1, 2, 3 and 4 we can find that a certain "stairs"-type elements connected to something what we can name "spirals". On the Fig. 5 we can see collected cross stich patterns, mainly from shirts of the area of the Ural mountain. Another never ending theme is the geometrical patterns what we can see on several very important buildings, e.g. on the walls of certain minarets. (Fig. 6). It is important to recognise that these geometrical patterns (many times one element in different rotational positions) are creating in their "inner space" (the area, which is not covered with the relief) possibilities to see certain other forms, patterns or elements. This type of visual experiences (including the investigation of old rock carvings) led us to the field of permutation-generated patterns. A small group of people (attracted by the high flame of the spirit of József V. Molnár, an artist, painter) started to work on the question, how to create a sign system, which contains the elements of the so called "organic" art.
Fig. 1 Cross stich pattern from the area of the river Tisza, Hungary
Fig.2 Cross stich pattern from the county Borsod, Hungary
Fig. 3 Image of an Aztec shield
Fig. 4 Clay vessel from Peru (Amano Museum, Lima) It is an open question (well, at least for me) what is the deeper reason to use the same elements together in different countries and times, what brings together these two elements (or symbols?) and what is the meaning what we can attach to them. Naturally, during the long years behind me with these signs, I have heard many different explanations and impressions – but still I am not feel settled about it. I started to understand more about the possible reasons when I was working longer time about the rather simple mathematics of the generation of the permutation-based signs.
Fig. 5 Cross stitch elements from the Ural area.
Fig. 6 pattern of the minaret in Üzkent, Turkey
2 The sign-system The inspiration arrived from certain rock-carvings. There are some frequently find elements of the screeched figures. We made some effort to put them in some "order". The next idea was to try to generate them, the next "we want to generate all"! Well, this is perhaps a little bit too ambitious plan, but we had some success, at least on some field.
Fig. 7 Schemas of rock carvings Working with the very simple mathematics of the idea of sign-creation, I realised that if we wont a system which can show (almost) everything, it has to be an endless system. The simplest thing in math, which can be a model of this, is the endless line of integers. Now, how to create (simple) forms or signs using integers? In a square matrix it is easy to this on a very simple way. The rule (worked out and worded only after longer time) is that in the rows and in the columns of an n×n square matrix (imagine simply graph paper) has to be from one to n (n can be any number) filled little squares. Look this little sign here. In a graph paper it would fill nine squares. It has three columns and three rows, it is a 3×3 little matrix. It is created according to the given rule. In the top row there is only one dark square, in the middle one there are three, in the lower one there are two. Similarly, in the first column (on the left) there are three, in the middle one there are two, on the right one there is one. From one to three we could find all the necessary squares. If we go higher with the numbers, and make "orderly" permutations, we can create a full system of signs. Putting them beside each other (here from the signs of n = 4) we can see symbols, very similar to Scandinavian deer-head motives, see Fig. 8.
Fig. 8
Fig. 9
Fig. 10 Another interesting experiment: let us take a sign from a table where n = 8 and the row vector is 1,2,3,4,5,6,7,8 the column vector is 4,5,3,1,2,6,8,7. Rotating the sign into the four possible position and putting them together, we can see totally different images if the directions of the rotation and the "going around" are opposing each other (Fig. 9) or they are the same (Fig. 10) Even such a simple mathematical model can show something about the behaviour of much bigger systems. (Perhaps Galaxies??) Actively looking around in it, and
working with this endless and amazing system, can improve our analogical
way of thinking. It can be great help when we try to understand the world
around us.
References Ditfurt, H., (1973), A világegyetem gyermekei, [Children of the Universe, in Hungarian] Budapest McIntyre, Loren, Mystery of the Ancient Nazca Lines, National Geographic, May, 1975 Molnár, V. J., (1999), Világ – Virág, [World-Flower, in Hungarian] , Budapest Purce, Jill, (1980), The Mystic Spiral, Thames and Hudson, London Spinden, H. J., (1975), A Study
of Maya Art,, Dover Publications, Inc., New York,
|