|
VIVA PHILOMORPH TOHRU OGAWA Name: Tohru Ogawa Address: University of Tsukuba, 3¾ 197, Edogawadai-Higashi, Nagareyama Email: ogawa-t@koalanet.ne.jp Phone & fax: +81-471-4714
Abstract: The aim of the presentation is multifold.
One is to discuss the relationship of the key concepts of interdisciplinary
activities. Another is to emphasize the importance of geometrical viewpoint.
1. PHILOMORPH, SYMMETRY, AND KATACHI The term PHILOMORPH (philos=loving, morphe=form) is not in dictionaries, but understandable referring to philosophy and morphology. Cyril Stanley Smith, who was originally a metallurgist and got interested in structural and aesthetic problems, coined the word (Smith 1981). Some common noun is desirable to express the comprehensive and synthetic interdisciplinary activities concerning symmetry, katachi, and others. Katachi is a Japanese word whose meaning is close to form, shape, appearance, figure, ... etc. It covers so wide range that nothing can be excluded in advance (Ogawa et al, 1996; Ogawa, 1996, 2000) as symmetry does (Nagy, 1990). Unfamiliar Katachi may be difficult to master perfectly on the Western background. Though the author himself regards katachi as the best Japanese translation of symmetry in the ISIS-Symmetry context, symmetry and katachi are two things. It is important to esteem the difference as well as the common between different cultures. Certainly, the dissymmetry makes the phenomenon as Currie claimed (Currie, 1894). Katachi is surely at some unique position to connect
everything in human activity. But the definition is not so sharp. It may
be the origin of the usefulness. To the contrary, symmetry in narrow sense
is well defined, even mathematical. The author regards the sharpness as
the origin of usefulness. Then he personally thinks that it is more scientific
than artistic.
2. GEOMETRY: MATHEMATICS, SCIENCE, AND CULTURE "For the last thirty or forty years, most Americans have somehow lost interest in Geometry. The present book constitutes an attempts to revitalize this sadly neglected subject," wrote H. S. M. Coxeter (Coxeter, 1961), as the preface to the first edition of his Introduction to Geometry. The neglect looks still going on though there are also some sign of opposite tendency. Most of students learn mathematics and physics only for
memory. Learning formula is only for exercise of calculation for them.
A basic formula contains everything in the field. Abundant information
can be drawn from it only if one desires and pays effort otherwise it stays
implicit. What should be learnt is not knowledge but how to enjoy, how
to have question, how to consider, how to put the meaning and then how
to draw information. Reminisce analytical geometry in which some coordinate
system is introduced and geometrical relations are expressed as equations.
Everybody can rewrite the equations. Where is the goal of rewriting? It
is OK if someone else gives the goal. Without purpose, one has nothing
to do. One may miss some important discovery unrecognized even when he
write some attractive expression by himself in a procedure if he is not
prepared. The most important is a kind of esthetic sense to penetrate the
interesting and the essential.
3. GEOMETRICAL ANALYSIS (CF. ANALYTICAL GEOMETRY) Different from analysis, geometry itself seems to have another possibility. Geometrical analysis as the opposite of analytical geometry, introduces some geometrical objects to analytical problems. What one should do is to try to exhaust its geometrical natures. To find some will be not hard although the perfect exhaustion is difficult. Let us take the allocation problem in electoral system
as an example. The detail of our approach to this problem will be presented
at another session in this congress (Ogawa and Ogawa,
2001). Suppose the basic principle of apportionment is known.
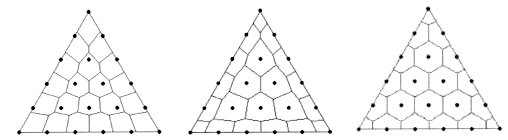
A regular triangle is symmetrically tessellated into twenty-one cells containing a lattice point in Fig. 1 - 3. What are the features of the tessellation? The author thinks it is not so difficult to guess some of them by observation though it is of course impossible to conclude rigorously. Set up some hypothesis and then connect the basic principle and the hypothesis logically applying analytical geometry. If it is successful then the meaning of the assumed feature should be studied. After getting familiar to the figure, it is easier to find other features. Thus one can experience an understanding of a whole system. Visualization made the recognition easy. Vision system always prepares some consistent model of the outside world even unconsciously for safety life in 3D space. It has evolved through the long history of life. The history of mathematics is negligibly short in comparison with that. Suppose one cannot find the feature of the figure by oneself. If he was taught the feature, he may be stimulated to go further by this hint. Overall comprehension gets easier by introducing geometry.
The verse "Let no one ignorant of geometry enter my door", which was over
the door of Plato’s academy, is reasonable from this point of view. It
also smoothly leads to the importance of Philomorph containing whole activity
of human being.
4. VISUAL vs. VERBAL Visual communication is so important that the proper position
is desirable to find in the system of Science and Philomorph. The proverb
says, ‘Seeing is believing.’ And ‘A picture is worth a thousand words.’
Of cause, the use of figures and illustrations is very helpful also in
Science. What kind of attention is necessary to pay in using figures and
illustrations for a scientific paper to be logical enough? The author should
not expect the readers to receive all the messages within a figure without
proper caption or proper description in the text. Sentences are one-dimensional
and then misunderstand by skipping some part is the fault of a reader.
Figure and illustration are another thing from it, since they are higher-dimensional
where the order of points are not unique and there is no guarantee that
the readers take correctly what the author intends. It is a problem of
logic. Though the establishing a logical system of figures is desirable,
it is also important to find proper verbal description of figures. It is
one of the important tasks of Philomorph as an extension of Science.
References H. S. M. Coxeter, Introduction to Geometry, (1961, 1969, John Wiley). P. Currie, J. de Physique, 3e série (1894), pp.393-415. D. Nagy, Symmetry: Culture and Science, 1, 3-26 (1990). T. Ogawa, K. Husimi, K. Miura, M. Masunari, and D. Nagy, in Katachi U Symmetry, Eds. T. Ogawa et al. (1996, Springer) T. Ogawa, in Katachi U Symmetry, Eds. T. Ogawa et al. (1996, Springer). T. Ogawa, Forma, 15, 1-10 (2000). T. Ogawa and T. Ogawa, in this Congress (2001). C. S. Smith, A Search for Structure,
(1981, MIT Press).
|
|||