|
POLYTOPIA PERFORMANCE CASPAR SCHWABE
Name: Caspar Schwabe Address: AHA, Spiegelgasse 14, 8001 Zürich, Switzerland E-mail: aha@datacomm.ch Fields of interest: Geometry, kaleidoscopes, polytopes, quasicrystals, golden mean, bionic, kinetic art. Exhibitions: Phenomena Expo Zurich, 1984; Heureka Swiss National Research Expo, 1991. Performances: Buckminster Fuller Symposium, RIBA,
London, June 2000; Bauhaus, Dessau, March 2001.
Abstract: The performance
of these shape-changing kinetic models has been considered to be a romance of many dimensions, a reference
to the famous 19th century Flatland by Edwin Abott. In the course
of unfolding them into three-spaces, they unveil interesting kinematic
phenomena like translation and rotation, explosion and implosion, inversion
and gastrulation, jitterbugging and tensegrity, knots and loops, and Moebius
strips. The polytope is the general term of the sequence point, diagon,
polygon, polyhedron, polytope. The chart below gives a good example of
the nature of the performance and the use of analogy in treating higher
dimensions. In Flatland the narrator is A Square; in comparison
the Chart deals with A Cube. Dimension implies direction and one can observe
the transformation of a cube in higher dimensions.
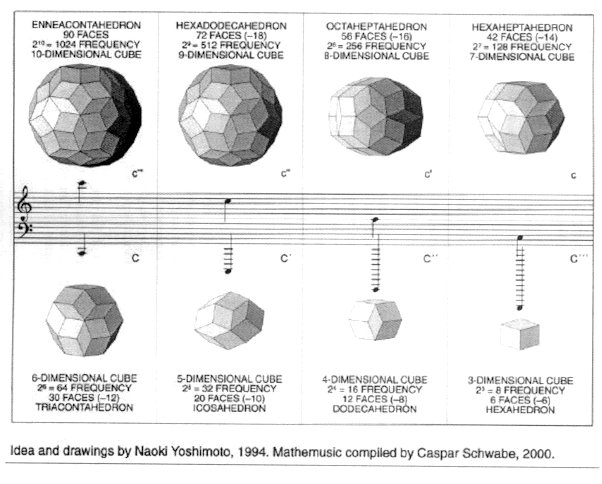
THE ZONOHEDRA MUSIC CHART The chart shows a set of Polyhedra, which are called zonohedra. A zonohedron is a convex polyhedron bounded by parallelograms. Johannes Kepler called a zonohedron "a polyhedron wearing a rhombus coat". Our Chart starts with the ninety-sided so-called 10-dimensional cube and ends with a six-sided 3-dimensional cube. The drawings of these solids are so called ortho-projections on a two-dimensional surface. Each of these zonohedra has a certain number of two kinds of rhombuses. The fat rhombus has a length/width ratio of 1 to Ö2 with an angle of 70.5 degrees (called a Maraldi angle) and the skinny rhombus has a ratio of 2 to (Ö5 + 3) with an angle of 41.5 degrees (centre angle of a dodecahedron).
Figure 1. As n being the starting dimension, we can generate the number of faces for the next zonohedron with the formula n x (n +1). Starting from zero dimension (a single point) the arithmo-geometrical generation goes like this: 0×1=0 faces, 1×2=2 faces, 2×3=6 faces, 3×4=12 faces, 4×5=20 faces, 5×6=30 faces, 6×7=42 faces, 7×8=56 faces, 8×9=72 faces, 9×10=90 faces, 10×11=110 faces, 11×12= 132 faces, etc. The Chart ends (or starts) with the 3-dimensional cube with 6 faces, 8 vertices and 12 edges. If we displace a cube (move it in space) and join the corresponding vertices of the first and second position by parallel lines, we get a hypercube with 24 faces, 16 vertices, 32 edges and 8 cells. A hypercube is called an 8-cell polytope or tesseract, meaning four rays, i.e. four dimensions. The main idea of our Chart is that the number of vertices of each zonohedra is exactly halved (or doubled) if we go to the next dimension. In the Chart the term 'vertices' is replaced by the term 'frequency' in accordance to the frequencies of the musical octaves. The Chart is a homage to the famous Pythagorean concept of the 'Harmony of the Spheres'. The Pythagoreans had discovered that the octave corresponds to the ratio 1 to 2 between the lengths of two vibrating strings. In the Pythagorean model of the universe, the sun and the planets revolve in concentric circles. The swift revolution of each of these bodies causes 'a musical hum' in the air. Evidently, each planet will hum in a different pitch, depending on the ratios of their respective orbits, just as the tone of a string depends on its length. Unfortunately, ordinary humans, even though being constantly bathed in this celestial humming, are lacking the gift of hearing the celestial music. The frequency of a sound per second is defined after the German physicist Heinrich Hertz with 'Hertz' (Hz). The lowest note C’’’ of our Chart cannot be perceived anymore by ear. It has a frequency of 8 Hertz, which corresponds to the eight vertices of a 3-dimensional cube. The first audible overtone C’’ (Subcontra C) has a frequency of 16 Hertz, which is an octave higher and corresponds to the 16 vertices of a hypercube. The whole Chart comprises seven octaves, very similar to a piano. The ratio of frequencies of each solid always corresponds to the number of vertices (or atoms) of a zonohedron. The polyhedral drawings and the idea of this type of zonohedra is a courtesy of Naoki Yoshimoto. When I came across his drawings in 1994, it became apparent to me that Yoshimoto’s search was following a similar line of ideas, which however I had not pursued to this perfection. So as a matter of fact, I was carrying the same idea in my mind for some time. Remark for the esoteric mind: The analogy between the zonohedra and the music should be perceived more by the intellect, not by the ear. For the mathematician: In four-dimensional space Euler's famous polyhedral formula (v + f = e + 2) can be completed to perfect symmetry: 16 vertices + 24 faces = 32 edges + 8 cells (v + f = e + c) ! For the scientist: Heinrich Hertz wrote that one cannot
escape the feeling that these mathematical formulae have an independent
existence and an intelligence of their own, that they are wiser than we
are, wiser even than their discoverers, that we get more out of them than
was originally put into them.
References (in chronological order) Kepler, Johannes (1619) Harmonices Mundi, Linz, Austria. Sharp, Abraham (1718) Geometry Improved, London, Great Britain. Kowalewski, Gerhard (1938) Der Keplersche Korper, Koehler, Leipzig, Germany. Coxeter, H.S.M. (1963) Regular Polytopes, Dover Publications (1973), New York, USA. Koestler, Arthur (1968) The Sleepwalkers, Pelican Books, London, Great Britain. Baer, Steve (1970) Zome Primer, Zomeworks Corporation, Albuquerque, New Mexico, USA. Yoshimoto, Naoki (1994) The Enneacontahedron, HyperSpace, Vol. 3, No.3, page 15, Kyoto, Japan.
Note from the editors: ISIS-Symmetry has a tradition of "artistic-scientific performances". Since Caspar Schwabe’s approach attracted a lot of interest during our past congresses, he became a "symmetric" (invariant) part of our events. Now we make a further step: Caspar will give a public lecture in the framework of the Congress, which will be open to a broader audience. The organizers are very thankful to the Pro Helvetia Foundation in Switzerland for supporting Caspar’s participation at the Congress and Exhibition in Sydney.
|