|
RANDOM SEQUENTIAL COVERING
TERUHISA SUGIMOTO and
Address: 1) Department of Statistical Science, The Graduate University for Advanced Studies, 4-6-7 Minami-Azabu, Minato-ku, Tokyo 106-8569, Japan. 2) The Institute of Statistical Mathematics, 4-6-7 Minami-Azabu, Minato-ku, Tokyo 106-8569, Japan. E-mail: Fields of interest: Geometry.
Abstract: In this
paper, the coverage problem on the sphere is studied. We consider the sequential
covering of identical spherical caps such that none of them contains the
center of another one. Set of such center points is said to form a Minkowski
set. We give an algorithm of random sequential covering under the condition
of Minkowski set.
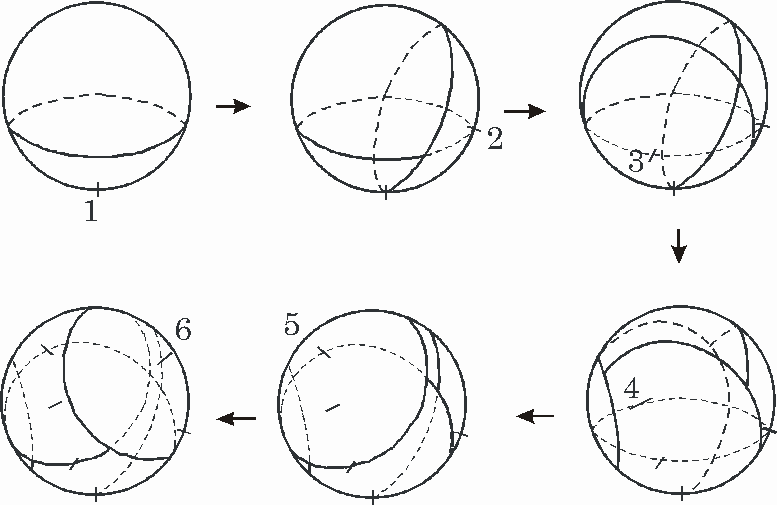
There are problems which deals with packing and covering of unit sphere by many identical spherical caps. These problems are applied to the globular histogenesis models of the biological organisms, to the uniform arrangement of observatories on the surface of the earth, to the information theories and so on. These problems have different features from the similar problems on the plane and there are unsolved and interesting problems. The coverage problem on the sphere is concerned mainly with the probability of complete coverage of the whole spherical surface. In the field of discrete mathematics, the interest is centered on getting the probability under the condition that the centers of spherical caps are chosen independently at random on the surface of the sphere. The problem here is such that the spherical caps may be put in the region already covered more than twice. Then, the coverage density often tends too high. We consider the sequential covering of spherical caps such that none of them contains the center of another one. Set of such center points is said to form a Minkowski set. We study the method of putting centers on the perimeter of already placed spherical caps as in the following steps: (1) The center of the first spherical cap is put at (x, y, z) = (0, 0, -1). (2) The center of the second spherical cap is chosen uniformly at random on the perimeter of the first spherical cap. The center of the third spherical cap is chosen uniformly at random on the part of the perimeter of the first spherical cap which is not covered by the second spherical cap. Repeat the above procedure, until the placed spherical caps cover the whole perimeter of the first spherical cap. (3) If the whole sphere has been covered, the procedure ends, else go to the next step. We call the uncovered regions the open concave regions. (Denote them by Ci , i=1,…,k; k is the number of open concave regions in this step.)
(4)The
center of a new spherical cap is chosen uniformly at random on the boundary
of the open concave regions (C1,…,Ck).
(Let us note that the boundary curves consist of the perimeter of spherical
caps and that they are not geodesic curves.) Repeat the above until the
boundary of the open concave regions (C1,…,Ck)
are all covered. Go to the step (3).
Fig.1. Sequential covering of spherical caps. Note: In the present method, there is a priority of choosing the centers on the boundaries of concave regions which existed in the step (3). There is another possibility of choosing the centers; namely, the centers of spherical caps are chosen uniformly at random from all boundary of the open concave regions which are present at the current stage. We obtained (theoretically) the angular radius and the positions of spherical caps such that the economical efficiency is the worst, in other words, such that the covering density is the highest under the condition of Minkowski set of centers.Incidentally, the solutions for spherical cap number 1, 2, 3, 4, 5, 6, 7, 10, 12, 14 were derived and proved when the economical efficiency is the best in the sequential covering. In the presentation, some results of computer simulation
according to our method will be given.
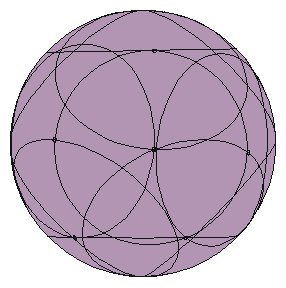
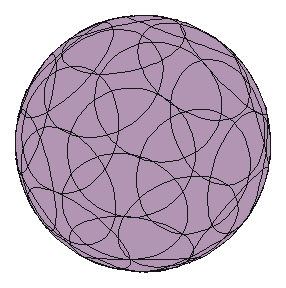
Angular radius is 0.80 [rad]. Angular radius is 0.50 [rad]. Fig. 2. Example of Computer
Simulation (View angle (-1,0,0)).
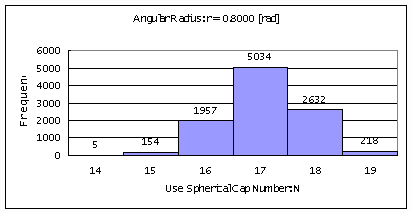
Table 1. Computer Simulation
for angular radius is 0.80 [rad].
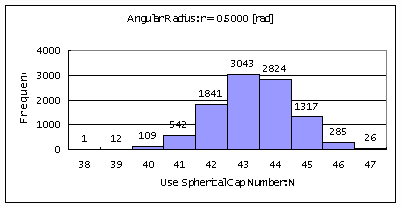
Table 2. Computer Simulation
for angular radius is 0.50 [rad].
References L. Fejes Tóth (1999) Minkowski Circle Packings on the Sphere, Discrete & Computational Geometry, 22, 161-166. G. Fejes Tóth (1969) Kreisüberdeckungen der Sphäre, Studia Scientiarum Mathematicarum Hungarica, 4, 225-247. L. Fejes Tóth (1972) Lagerungen in der Ebene
auf der Kugel und im Raum, 2nd ed, Springer-Verlag, Berlin, Heidelberg,
New York.
|