Name: Tibor Tarnai, Structural Engineer, Applied Mathematician, (b. Hatvan, Hungary, 1943). 

Address: Department of Structural Mechanics, Budapest University of Technology and Economics, Müegyetem rkp. 3, Budapest, H-1521 Hungary. 

E-mail: tarnai@ep-mech.me.bme.hu

Fields of interest: Kinematically indeterminate structures, discrete geometry (packing and covering problems).

Awards: Medal of Department of Architecture Kyoto University, 1997.

Publications: 

Tarnai, T. (1996) Symmetry of golf balls, In: Ogawa, T., Miura, K., Masunari, T. and Nagy, D., eds,. Katachi U Symmetry. Tokyo: Springer-Verlag, 207-214.

Tarnai, T. (1996) Geodesic domes: Natural and man-made, International Journal of Space Structures, 11, 13-25.

Tarnai, T. (1997) Folding of uniform plane tessellations, In: Miura, K. ed., Origami Science and Art, Procceedings of the Second International Meeting of Origami Science and Scientific Origami, Otsu: Seian University of Art and Design, 83-91.

Fowler, P.W. and Tarnai, T. (1999) Transition from circle packing to covering on a sphere: The odd case of 13 circles, Proceedings of the Royal Society of London, A 455, 4131-4143.

Tarnai, T. and Gáspár, Zs. (2001) Packing of equal regular pentagons on a sphere, Proceedings of the Royal Society of London, A 457, 1043-1058.
 
 

Abstract: How must n equal non-overlapping regular spherical pentagons be packed on a sphere so that the angular radius of the circumcircles of the pentagons will be as great as possible? This problem is analogous with the Tammes problem of the densest packing of equal circles on a sphere. A closely related problem is: How must n equal non-overlapping regular pentagons be packed in a circle so that the circumradius of the pentagons will be a maximum? – that is analogous to the problem of the densest packing of equal circles in a circle. In this paper we will deal with the pentagon packing problems, but a comparison will be made between the conjectured solutions to the circle packing problems and the pentagon packing problems. This comparison has a special interest where the packings on a sphere have tetrahedral, octahedral or icosahedral symmetry. Applications of different packings will also be presented. 
 
 

1 CIRCLE PACKINGS

The problems of the densest packing of equal circles in the plane, in a circle and on a sphere are well known. Though the problem in the plane is solved, the solution in a circle and on a sphere is known only for certain numbers of circles. An intensive survey of the literature of the circle packing problems is given by Fejes Tóth (1972), Croft et al. (1991) and Conway and Sloane (1998). The best circle arrangements on a sphere have been presented by Kottwitz (1991), but those under tetrahedral, octahedral and icosahedral symmetry constraints by Tarnai and Gáspár (1987). Recently, the list of the best spherical circle packings, with and without icosahedral symmetry constraints, was extended by R.H. Hardin, N.J.A. Sloane and W.D. Smith for up to n = 2072 and 130, respectively, and the results are available on the Internet (http://www.research.att.com/~njas). The known best arrangements of equal circles in a circle for up to n = 65 are given in Graham et al. (1998).

It turns out that there is a correspondence between the arrangements found in solutions and conjectured solutions of these packing problems and many distinct physical, biological and engineering structural problems (Tarnai and Gáspár, 2000). For instance, the infinite packing in the plane is represented in crystal structures; finite packings in a circle occur as fruit arrangements in lotus receptacles, or wire arrangement in cables of suspended bridges (Tarnai, 2001); circle packings on a sphere correspond to the distribution of pores of spherical pollen grains, or to dimple patterns of golf balls (Tarnai, 1984). Circle packings in the plane, in a circle and on a sphere occur as motifs also in art.
 

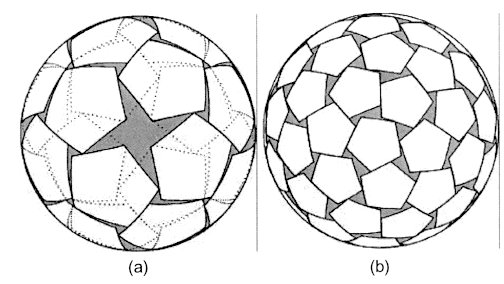
2 PENTAGON PACKINGS

Contrary to the packing of equal circles, we do not know the densest packing of equal regular pentagons in the plane. Only a conjecture is published for the best arrangement of pentagons in the plane (Henley, 1986), though the suggested arrangement has been known for a long time as an ice-ray pattern in Chinese lattice design. In physics of condensed matter, it is a problem, how packing of uniform elements is crystallized. For that purpose, in air-table experiments equal regular pentagons were used, which formed large blocks with the arrangement conjectured by Henley (Limon Duparcmeur et al., 1995).

For finite packing of pentagons, we can ask how to arrange a given number of non-overlapping equal pentagons in a circle so that the size of the pentagons will be a maximum. In mathematics this problem has not yet been investigated. Nature, however, provides examples of such packings. For instance, the shrub-like plant Phlomis fruticosa has flowers in whorls, where each flower is sitting in a tubular calyx with 5 teeth. After the petals fall down, the arrangement of calyxes is like packing of equal five pointed stars or pentagons in a circular domain (Clauser and Innocenti, 1999). 

Close packing of a given number of equal pentagons can be arranged also on the surface of a sphere. Here the following mathematical problem arises: How must n non-overlapping regular spherical pentagons be packed on a sphere so that the angular radius of the circumcircles of the pentagons will be as great as possible? The spherical circle-packing problem has a vast literature. In contrast, apart from some work by the author, the spherical pentagon-packing problem has no literature. Conjectured solutions to the spherical pentagon packing problem without symmetry constraint have been established for up to n = 12, and with octahedral and icosahedral symmetry constraints for n = 24 and 72, respectively, were presented by Tarnai and Gáspár (2001). The results for the last two are shown in Figure 1.

It turns out that there are physical situations where spherical pentagon packings occur. For instance, in architecture. There are equal regular pentagonal openings on the spherical dome of the Haseki Hürrem Sultan Bath near Hagia Sophia at Sultan Ahmet Square in Istanbul (built by Mimar Sinan in the 16^th century) where they are arranged along small circles of the sphere. An example in art is a sculpture of István Kiss, set up in Salgótarján, Hungary in 1985, where equal regular pentagons are randomly arranged on the surface of a sphere. But some temari balls in Japan also have pentagon packing decoration. In biology, structures of "all-pentamer" viruses have particular importance in this respect (Baker et al., 1991). We have shown that the arrangements of pentamers of papillomaviruses, taking concentric spherical sections of the twisted subunits at two extreme radii, correspond to two locally optimal (closest) packings of 72 equal pentagons on a sphere under the constraint of icosahedral symmetry. One of them is shown in Figure 1(b). Additionally, some viruses take a swollen form if acidity of their environment changes. We have constructed a mechanical model to simulate this phenomenon. It is an expandable regular dodecahedron (Kovács and Tarnai, 2000).
 

Acknowledgement. Research reported here was supported in parts by OTKA Grant No. T031931, and by OMFB and the British Council Grant No. GB-15/99.

References