|
PARABOLA DRAWING METHODS IN TRADITIONAL JAPANESE ARCHITECTURE HIROSHI YANAI Name: Hiroshi Yanai,. Operational Research Analyst, Mathematician, (b. Tokyo, Japan , 1937) Address: Department of Science and Technology,
Keio University, 3-14-1 Kohoku-ku,
E-mail: yanai@ae.keio.ac.jp Fields of interest: Operational Research, Traditional Architecture, Mathematics. Awards: Ohnishi Memorial Prize (Operations Research Society of Japan), 1968; Prize for Applications of Operations Research (Operations Research Society of Japan), 1983.
Publications and/or Exhibitions: Yanai, H. and Okamura, Kiyoshi (1988) Curves of roofs in traditional Japanese architectures, Asian–Pacific Operations Research: APORS’ 88, Elsevier, 597-619. Yanai, H. (1988) Curves of jacket walls, [in Japanese], Operehshonzu Risahchi, 33, No. 6. Yanai, H. (1991) Curves of roofs in traditional Japanese architecture, [in Japanese], Operehshonzu Risahchi, 36, No. 6. Yanai, H. (1993) An Essay on the Connotations by Curved Roofs in Traditional Japanese Architecture, [in Japanese], Technical Report No. 93002, Tokyo: Keio University. Yanai, H. (1998) On some ruled surfaces, [in Japanese], Suhri–kagaku, No. 6. Yanai, H. (1999) Curves in traditional Japanese architecture and civil engineering, Forma, 14, 331-338. Yanai, H. (1999) Curves shaped from strings, [in Japanese], Suhri–kagaku, No.11. Yanai, H. (2001) Curves in traditional architecture in
East Asia, Mathematical Intelligencer, 23, No.1, 52-53.
Abstract: Some drawing
procedures of the curves of stone walls in Japanese castles are described
in the manuscripts of the Gotoh family written in early 17 century. These
procedures are based on constructing parabola with horizontal axis as an
envelope of a set of straight lines made by spanned strings. The origin
of such procedures is conjectured to be in Ying
zao fang shi published in 1078 in China, in which an envelope is used
to construct the curve of the wooden support between pillar and beam. The
validity of this conjecture is to be discussed in this paper.
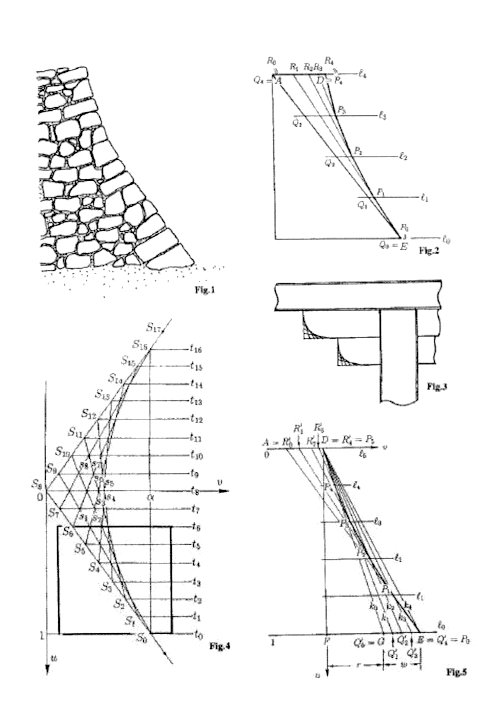
Most of the jacket walls of Japanese castles were built as stone covering on steepened slopes of hills upon which castles were built. They are shaped into concave, peculiar curves called sori (Fig. 1). Some constructing, viz. drawing procedures are described in the manuscripts of the Gotoh family written in early 17 century. Translating the procedure into "Western" mathematics, it is corroborated that these procedures are based on constructing parabola with horizontal axis as an envelope of a set of straight lines of spanned strings. The straight lines are determined by connecting their ends at given points: the upper points are constituting diminishing arithmetic sequence on the horizontal plank overhanging from the summit of the slope, while the lowers are given at the wall-side edges of the scaffolds. The scaffolds are piled up stage by stage in a constant height, while the stones are piled up along the "newly" spanned strings (Fig. 2). There arises, however, a question how Gotohs are arrived at such an elaborate procedure without knowledge of modern mathematics. A hint is in Ying zao fang shi, a Chinese canonical textbook on architecture published in 1078 under the permission by the emperor of China, which is presumed to be widespread over East Asian World. In this book a method called Juan sha is described to use an envelope to construct the curve of the wooden support between pillar and beam. Equidistant points are marked along each of two rectangular edges of a wooden block. The straight lines connecting the points on the two sides are sawn to constitute a parabolic curve as the envelope and a convex parabolic wooden support is obtained (Fig. 3). The angle between the two edges of the original wooden block is rectangular in most of the cases. However, if we broaden the angle, we obtain various parabolas of various curvatures, among which we would be able to find some suited for jacket walls. But since the curve of a jacket wall is a part of the half parabola, it is necessary to cut out a part from the envelope. And in order to map the straight lines to the real scale of the jacket wall, it is necessary to determine the end points of the spanned strings. Lower ends are equidistantly distributed in heights. As for the upper, horizontal distances among the end points, as it is inferred, are measured from the figure at the height corresponding to the plank to realize to constitute a diminishing arithmetic sequence (Fig. 4). However, this hypothesis is nothing more than a conjecture
and there is no way to give the evidence today. It is necessary to try
a debate with another counter hypothesis. A possible counter hypothesis
is the method of gradation used to form the curve of Chidori gable
in traditional Japanese architecture, which is also parabolic. Based on
this method it is theoretically possible to construct a procedure of forming
the curve of jacket wall in which a set of equidistantly distributed points
at the bottom is connected to the uppermost vertex of the jacket wall to
obtain a set of rays. These rays are cut by a set of equidistantly distributed
horizontal straight lines of the same number as the rays to obtain the
points of intersections among rays and straight lines in corresponding
order. Connecting thus obtained points of intersections we obtain connected
line segments which tend to a parabola by infinitely increasing the number
of the rays and straight lines. In order to obtain the points on the plank,
however, the line segments connecting the corner point at the bottom and
the points of intersection must be extrapolated to the level of the plank
(Fig. 5).
Debate between these two hypotheses, Juan sha and Chidori gable hypotheses, are attempted from various points of view: technological genealogy, technical feasibility, reasonability in way of thinking, trace of constructing the procedure examining the parameters.
References Takeshima, T (1970-72) A Study on "Ying zao fang shi", [in Japanese], Vols.1-3, Chuo-kohron Bijutsu Morinaga, T. (1975) Illustrations of Traditional Architectural Techniques, [in Japanese], Kinryu-do. Ichikawa, K. (1960) Science of Creations, [in Japanese], NHK Press. Kitaoka, Y. (1999) Curves of Roofs of Ancient and Middle Age Temples and Shrines, [in Japanese], Private edition. Yanai, H. (1988) Curves of jacket walls, [in Japanese], Operehshonzu Risahchi, 33, No. 6. Yanai, H. (1991) Curves of roofs in traditional Japanese architecture, [in Japanese], Operehshonzu Risahchi, 36, No. 6.
|