THE GOLDEN NUMBER IN THE HARMONY OF WHAT
IS CREATED
The Golden Number (F =1.6180339...) is the measure of the perfect proportion between two unequal parts. Known since a very remote antiquity, in the plane geometry Vitruvio proposed that "so that a space divided into unequal parts results pleasant and aesthetic, the relation between the smallest and the largest part must be the same as between the largest and the whole". Regarding linear systems Euclides defined that such proportion is the "division of one length in medium and extreme ratio" or Golden Section. As explained by Ghyka, that code of nature rather than being fully described it exhibits in the unstable concourse of all the parts of the living beings and on the matter with some form of dynamic structures, with the expression of the summarized numeric pattern that is F, with the basis of the number 5. Rather, in the forms of the matter not organized for life, in the exponents of stable symmetries and in the structures of crystalline balance its numeric scheme resorts in general to the number 6. THE PROPORTIONS IN ARCHITECTURE In the architectural creation the best harmony of the composing parts of a work incorporate F connatural to man due to being in its same proportions. The human being has applied criteria developed on that harmony in spontaneous or voluntary form in the best of its creation since the antiquity, in the cultures of Sumer, Egypt and Tiwanaku; and, in Occident, starting with the studies of Policleto, Euclides and Vitruvio, those of Alberti, Leonardo da Vinci, Durero, Miguel Angel, Zeising and Le Corbusier, among many others. The architect expresses by intuition the concept of the
‘desired design’ and, according to Le Corbusier, "automatically makes the
necessary optic corrections", in addition to what was addressed by Leibniz
regarding the application of the pre-existing harmony, as "we own much
knowledge of what we do not have clear conscience even when we apply it
"assuming that "all the arithmetic and all the geometry exist in an innate
and virtual in our soul", although "the innate principles only appear when
the attention is fixed on them".
FIN THE CONFIGURATION OF THE HEN'S EGG
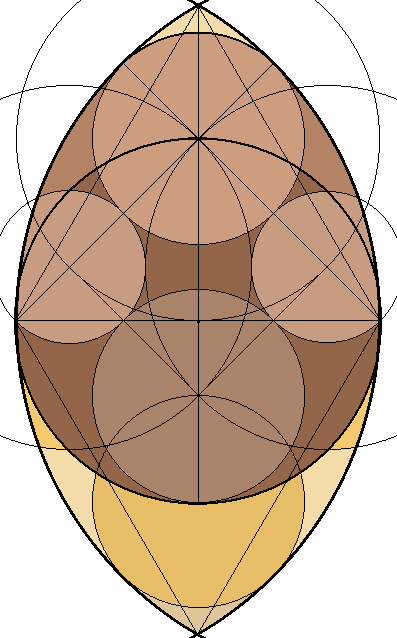
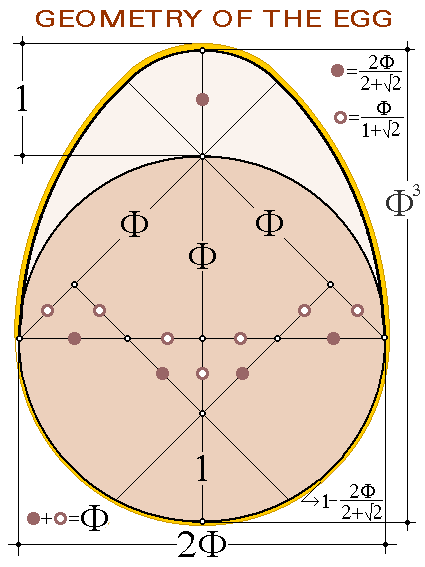
NON-PARABOLIC GEOMETRY IN THE OVAL SECTION The drawing with arcs of four circles is the one that
better configure the oval inscribed in the vesica piscis. Though
in this drawing there is no parabola, it has with exactness the proportions
of its chord and sagitta. The tiny difference between the parabola and
the combination of circular arcs in non significant parts (see graphic
of the parabola) makes that the product of the analysis of the oval figure
serves for the fast design of the parabolic and pointed arcs and for a
higher knowledge of the parabola.
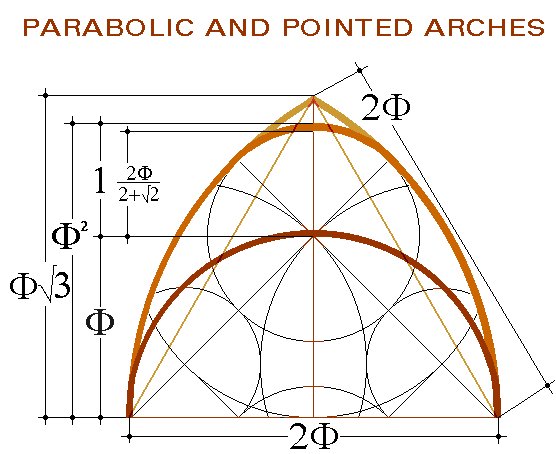
GEOMETRY OF THE POINTED AND PARABOLIC ARCHES
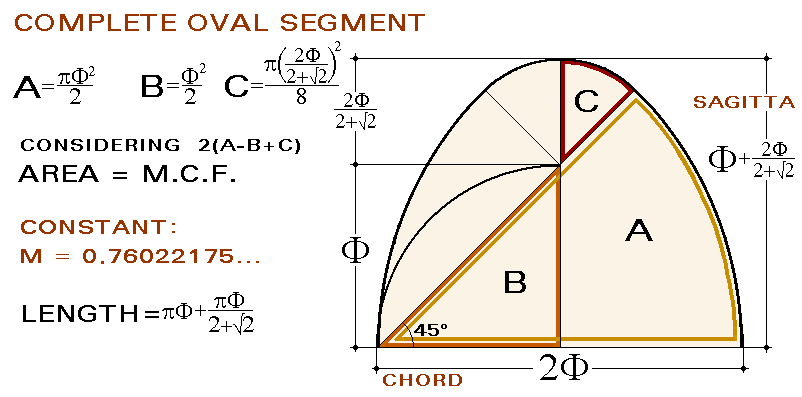
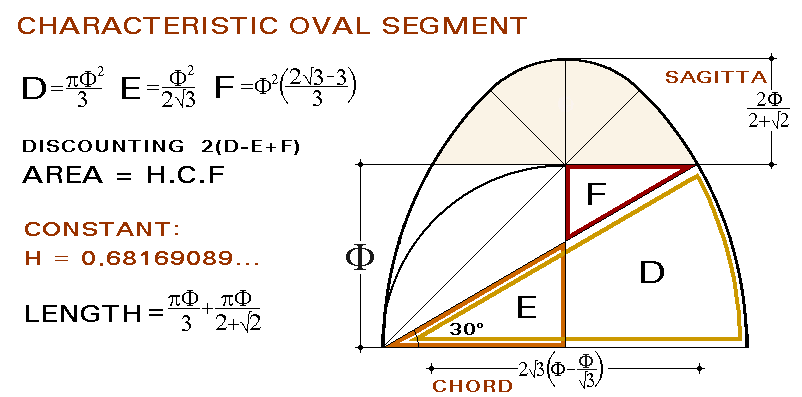
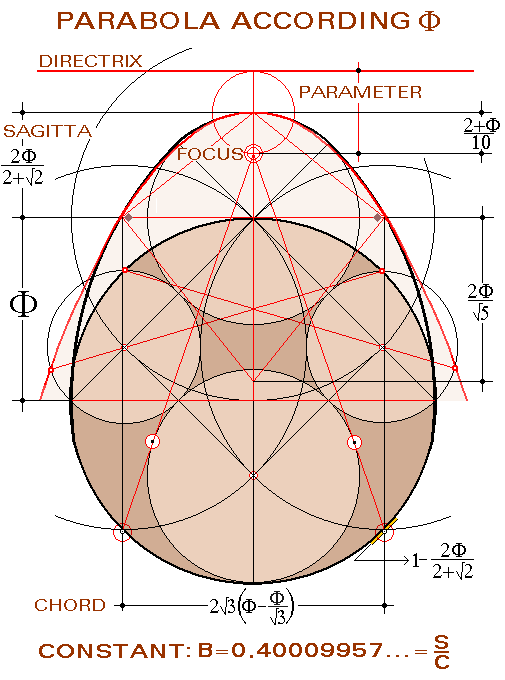
GEOMETRY OF THE PARABOLA ACCORDING TO F All parabolas are similar: while the size varies, the constants of their configuration are the same for all them. Consequently, having demonstrated that the parabola is on the oval section configured by F, the relative proportion of the main dimensions of every parabola are established: parameter, sagitta and chord, with the subsequent implications. Also the harmonic coherence of the joint assembly that associates the oval figure with the parabola permits to confirm the location of the focus of it.
|