|
BETWEEN ART AND NATURE? RICHARD P. TAYLOR1, BEN R.
NEWELL2,
1) Physics Department, University of Oregon, Eugene, 97403, USA 2) Department of Psychology, University College London, London, UK 3) School of Psychology, University of New South Wales, Sydney, 2052, Australia 4) Centre for Cognitive Science, Macquarie
University, Sydney, 2109, Australia
Name: Richard Taylor is an Associate Professor
of Physics at the University of Oregon, USA. Since gaining his Ph.D. in
experimental physics in 1988, he has published over 125 research papers
in international journals and has worked in the USA, UK, Canada, Japan
and Australia. In addition, he has trained as a painter at the Manchester
School of Art, U.K., and has a Masters Degree in Art Theory. His research
interests focus on fractals in a range of physical systems and also on
the scientific analysis of abstract art. He currently is writing a book
on the Art, Science and Psychology of Jackson Pollock's drip paintings.
Abstract: Fractal geometry
has experienced spectacular success in quantifying the complex structure
exhibited by many natural patterns, including coastlines, trees and clouds
(Mandlebrot, 1977). In contrast to the simplicity of
Euclidean shapes, the complexity of fractal patterns results from the recurrence
of patterns at finer and finer scales. Here we show that humans display
a consistent aesthetic preference across fractal images, regardless of
whether these images are generated by nature’s processes, by mathematics,
or by humans. We discuss the implications of this result for the artist
Jackson Pollock, whose drip paintings we recently showed to be fractal
(Taylor et al, 1999).
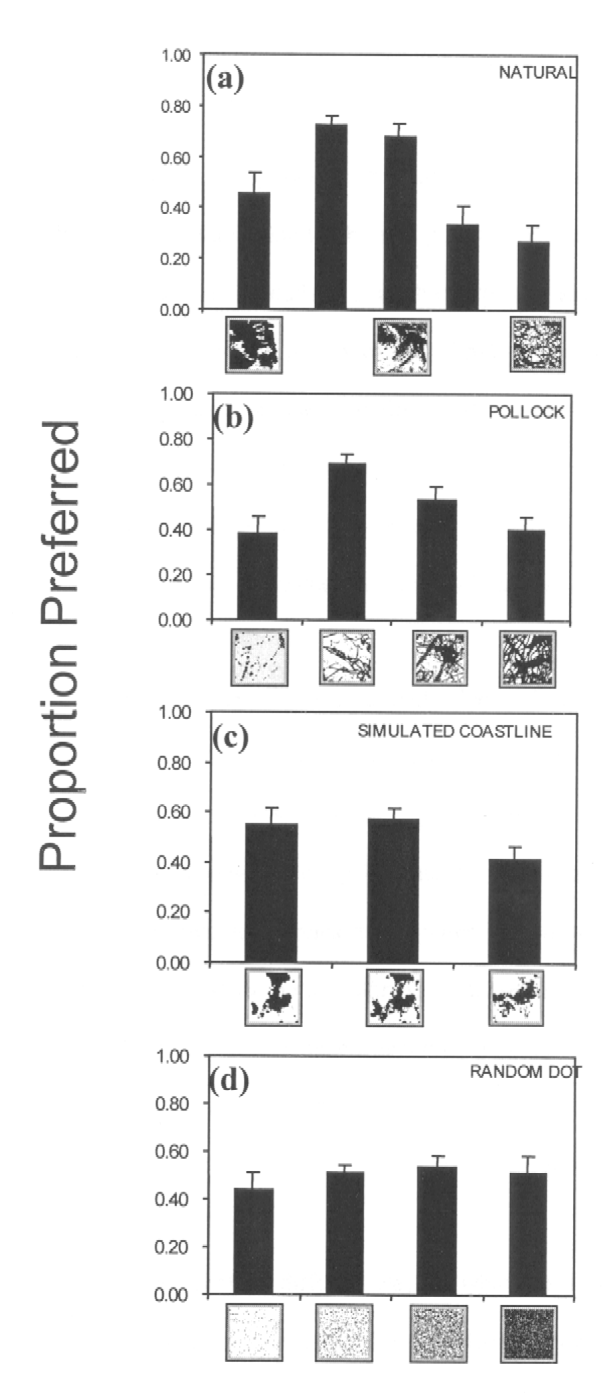
The study of human aesthetic judgement in general, and of fractal patterns in particular, constitutes a relatively new research field within perceptual psychology. Previous studies of fractal objects have focussed predominantly on how fractal character influences perceived visual qualities such as roughness and complexity. Only recently has research started to quantify people's visual preferences for (or against) fractal content. To determine if there is any universal aesthetic quality of fractals, we have carried out a comprehensive study incorporating three categories of fractal pattern: 1. natural fractals - scenery such as trees, mountains, waves, etc; 2. mathematical fractals - computer simulations of coastlines; 3. human fractals - cropped sections of paintings by the artist Jackson Pollock that have recently been shown to be fractal (Taylor et al, 1999). The fractal character of an image can be quantified by a parameter called the fractal dimension, D. This parameter quantifies the fractal scaling relationship between the patterns observed at different magnifications (Mandlebrot, 1977). For Euclidean shapes, dimension is a familiar concept described by integer values. For a smooth line (containing no fractal structure) D has a value of 1. For a completely filled area (again containing no fractal structure) its value is 2. For fractal patterns, D lies in the range between 1 and 2 with a value depending complexity and richness of the repeating structure. Here, we used 15 computer-generated images of simulated coastlines (Mandlebrot, 1977), 5 each with D values of 1.33, 1.50 and 1.66; 40 cropped images from Jackson Pollock’s paintings, 10 each with D values of 1.12, 1.50, 1.66 and 1.89; and 11 images of natural scenes with D values ranging from 1.1 to 1.9. All the images were black and white, and in the case of the natural and Pollock stimuli, presented in such a way as to disguise their identity. Initially, visual preferences for images within the same category and with the same fractal dimension were compared using a forced-choice visual preference task. Participants indicated their preference from one of two images appearing on a monitor. All images were paired with each other and preference was quantified in terms of the proportion of times each image was chosen. At this stage, the most and least preferred images were excluded from further comparisons, which led to the selection of the two most representative images for each fractal dimension within each category. Using these representative images, visual preferences were then compared across fractal dimensions. Panels a, b and c of the figure show that, across the three different origins of fractal image there is a consistent aesthetic preference for images with a fractal dimension in the range 1.3 to 1.5. Taken together the results indicate that we can establish three categories with respect to aesthetic preference for fractal dimension: 1.1-1.2 low preference, 1.3-1.5, high preference and 1.6-1.9 low preference. In contrast to this pattern, panel d shows that there was no preference across a set of computer generated random dot patterns with no fractal content but matched in terms of density (area covered) to the low, medium and high fractal patterns, demonstrating that aesthetic preference is indeed a function of fractal dimension and not simply density. Our analysis extends previous studies that have concentrated
on only one category of fractals (Pickover, 1995; Aks
& Sprott, 1996), demonstrating an aesthetic preference for a particular
fractal character across fractal images of distinctly different origins.
Given that fractals define our natural environment, the identification
of the fractal characteristic determining aesthetic preference could be
of fundamental importance in understanding the way in which our perception
in general and our appreciation of art in particular are shaped by the
world around us.
Figure 1: Aesthetic preference for fractal
images.
References Aks, D.J. & Sprott, J.C. (1996)
Quantifying Aesthetic Preference for chaotic patterns. Empirical Studies
of the Arts, 14, 1-16.
Mandelbrot, B.B. (1977) The Fractal Geometry of Nature, Freeman, New York. Pickover, C. (1995) Keys to Infinity, Wiley, New York. Taylor, R.P., Micolich, A.P. & Jonas,
D. (1999) Fractal analysis of Pollock's drip paintings, Nature,
399, 422.
|